Using a Hidden Markov Model with Poisson Emissions to Understand Earthquakes

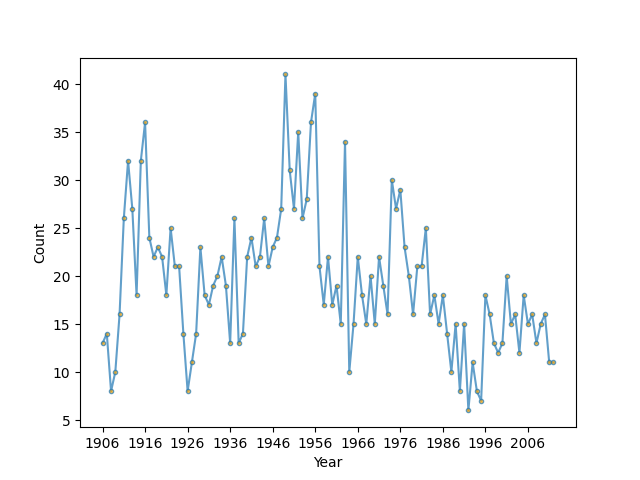
Let’s look at data of magnitude 7+ earthquakes between 1900-2006 in the world collected by the US Geological Survey as described in this textbook: Zucchini & MacDonald, “Hidden Markov Models for Time Series” (https://ayorho.files.wordpress.com/2011/05/chapter1.pdf). The goal is to see if we can separate out different tectonic processes that cause earthquakes based on their frequency of occurance. The idea is that each tectonic boundary may cause earthquakes with a particular distribution of waiting times depending on how active it is. This might tell help us predict future earthquake danger, espeically on a geological time scale.

import numpy as np
import matplotlib.pyplot as plt

from scipy.stats import poisson
from hmmlearn import hmm

# earthquake data from http://earthquake.usgs.gov/
earthquakes = np.array([
    13, 14, 8, 10, 16, 26, 32, 27, 18, 32, 36, 24, 22, 23, 22, 18,
    25, 21, 21, 14, 8, 11, 14, 23, 18, 17, 19, 20, 22, 19, 13, 26,
    13, 14, 22, 24, 21, 22, 26, 21, 23, 24, 27, 41, 31, 27, 35, 26,
    28, 36, 39, 21, 17, 22, 17, 19, 15, 34, 10, 15, 22, 18, 15, 20,
    15, 22, 19, 16, 30, 27, 29, 23, 20, 16, 21, 21, 25, 16, 18, 15,
    18, 14, 10, 15, 8, 15, 6, 11, 8, 7, 18, 16, 13, 12, 13, 20,
    15, 16, 12, 18, 15, 16, 13, 15, 16, 11, 11])


# Plot the sampled data
fig, ax = plt.subplots()
ax.plot(earthquakes, ".-", ms=6, mfc="orange", alpha=0.7)
ax.set_xticks(range(0, earthquakes.size, 10))
ax.set_xticklabels(range(1906, 2007, 10))
ax.set_xlabel('Year')
ax.set_ylabel('Count')
fig.show()

Now, fit a Poisson Hidden Markov Model to the data.

scores = list()
models = list()
for n_components in range(1, 5):
    for idx in range(10):  # ten different random starting states
        # define our hidden Markov model
        model = hmm.PoissonHMM(n_components=n_components, random_state=idx,
                               n_iter=10)
        model.fit(earthquakes[:, None])
        models.append(model)
        scores.append(model.score(earthquakes[:, None]))
        print(f'Converged: {model.monitor_.converged}\t\t'
              f'Score: {scores[-1]}')

# get the best model
model = models[np.argmax(scores)]
print(f'The best model had a score of {max(scores)} and '
      f'{model.n_components} components')

# use the Viterbi algorithm to predict the most likely sequence of states
# given the model
states = model.predict(earthquakes[:, None])

Converged: True         Score: -391.9189281654951
Converged: True         Score: -391.9189281654951
Converged: True         Score: -391.9189281654951
Converged: True         Score: -391.9189281654951
Converged: True         Score: -391.9189281654951
Converged: True         Score: -391.9189281654951
Converged: True         Score: -391.9189281654951
Converged: True         Score: -391.9189281654951
Converged: True         Score: -391.9189281654951
Converged: True         Score: -391.9189281654951
Converged: True         Score: -341.89397049875447
Converged: True         Score: -341.88244772721396
Converged: True         Score: -342.14454823785394
Converged: True         Score: -341.89296748597104
Converged: True         Score: -341.8855538199331
Converged: True         Score: -342.28762276127594
Converged: True         Score: -342.5369292103581
Converged: True         Score: -341.88750207762195
Converged: True         Score: -341.87893633799735
Converged: True         Score: -342.9703881743685
Converged: True         Score: -343.0429169039876
Converged: True         Score: -342.0845203955183
Converged: True         Score: -342.6892743201989
Converged: True         Score: -328.5977427805315
Converged: True         Score: -341.6613001106409
Converged: True         Score: -329.0639942771591
Converged: True         Score: -329.5050253557605
Converged: True         Score: -338.90786993240823
Converged: True         Score: -328.7562782189667
Converged: True         Score: -337.65157449610496
Converged: True         Score: -328.140456803197
Converged: True         Score: -340.59777383065614
Converged: True         Score: -330.4670538297964
Converged: True         Score: -341.5633429271246
Converged: True         Score: -328.02126544237626
Converged: True         Score: -340.86474747756444
Converged: True         Score: -339.55978555721845
Converged: True         Score: -328.69847130568786
Converged: True         Score: -328.87604629227917
Converged: True         Score: -340.1318877583548
The best model had a score of -328.02126544237626 and 4 components

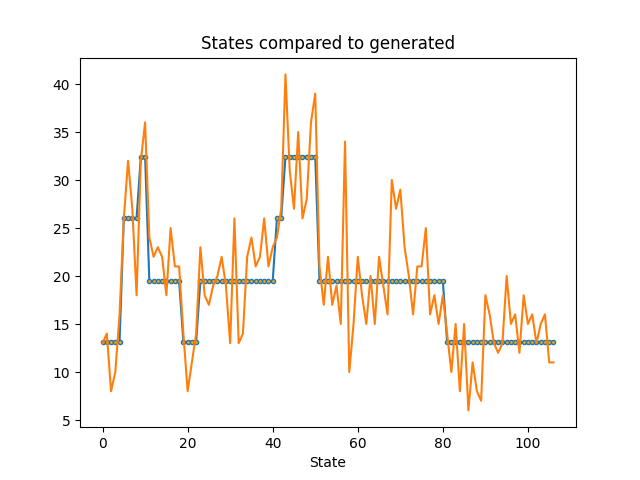
Let’s plot the waiting times from our most likely series of states of earthquake activity with the earthquake data. As we can see, the model with the maximum likelihood had different states which may reflect times of varying earthquake danger.

# plot model states over time
fig, ax = plt.subplots()
ax.plot(model.lambdas_[states], ".-", ms=6, mfc="orange")
ax.plot(earthquakes)
ax.set_title('States compared to generated')
ax.set_xlabel('State')

Text(0.5, 23.52222222222222, 'State')

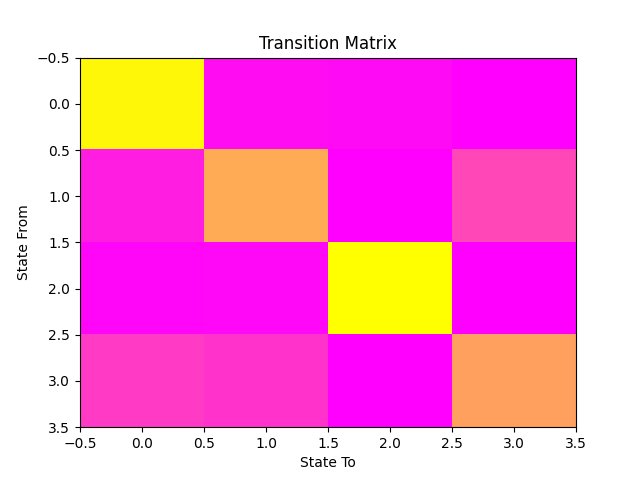
Fortunately, 2006 ended with a period of relative tectonic stability, and, if we look at our transition matrix, we can see that the off-diagonal terms are small, meaning that the state transitions are rare and it’s unlikely that there will be high earthquake danger in the near future.

fig, ax = plt.subplots()
ax.imshow(model.transmat_, aspect='auto', cmap='spring')
ax.set_title('Transition Matrix')
ax.set_xlabel('State To')
ax.set_ylabel('State From')

Text(31.222222222222214, 0.5, 'State From')

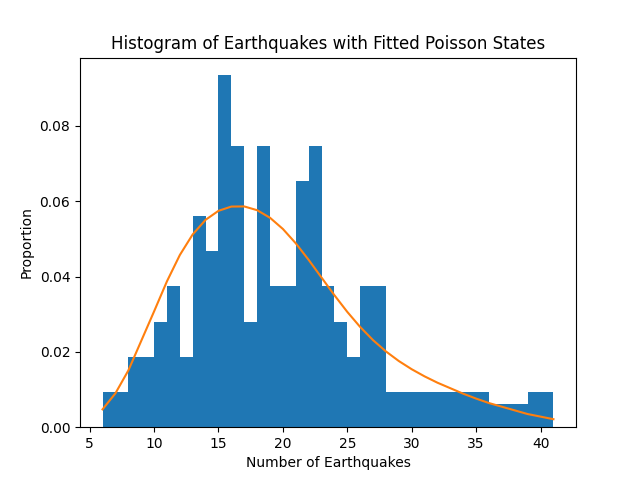
Finally, let’s look at the distribution of earthquakes compared to our waiting time parameter values. We can see that our model fits the distribution fairly well, replicating results from the reference.

# get probabilities for each state given the data, take the average
# to find the proportion of time in that state
prop_per_state = model.predict_proba(earthquakes[:, None]).mean(axis=0)

# earthquake counts to plot
bins = sorted(np.unique(earthquakes))

fig, ax = plt.subplots()
ax.hist(earthquakes, bins=bins, density=True)
ax.plot(bins, poisson.pmf(bins, model.lambdas_).T @ prop_per_state)
ax.set_title('Histogram of Earthquakes with Fitted Poisson States')
ax.set_xlabel('Number of Earthquakes')
ax.set_ylabel('Proportion')

plt.show()